在之前的机器学习和神经网络中,对于非线性变换/激活函数比较常用的是 sigmoid, tanh 等这类比较 smooth 而且 被 bound 住的函数。然而目前,在深度学习尤其是卷积神经网络中,用的最多的是 ReLU 函数。直观上看,ReLU 是一个分段的线性函数,因此,就很容易想到 ReLU 应该不像 sigmoid 和 tanh 等这类 smooth & bounded 的函数那样 powerful, 换句话说,ReLU 的效果应该比较差。然而,在实际应用中,ReLU 的效果要比 sigmoid 这类 smooth & bounded 的函数效果要好很多。经过现实的打脸之后,不禁要问,底为什么 ReLU 的效果会比 sigmoid 好呢?
首先还是要明确一下 ReLU 函数:
\[ ReLU\left(x\right)= \left\lbrace \begin{align} x, \quad x \gt 0 \cr 0, \quad x \le 0 \end{align} \right . \]ReLU 的输出要么是 0, 要么是输入本身,极其简单。如果没有实验结果打脸,那么,我第一反应就是这个函数太简单,根本学不到什么东西。但是,实验结果的打脸促使进一步的思考,为什么 ReLU 如此简单,却可以真正 work, 而且,其效果还要比 sigmoid / tanh 等这些传统的,经典的激活函数好。
可以类比一下 Boost 算法,把 ReLU 看成是一个分段的,用来 separate 数据的函数,而不是一个去真正的拟合某个函数。在机器学习中,数据集都是有限的,所以,通过去分割数据空间,只要分割的次数足够多,那么,总是可以得到正确的分割结果。
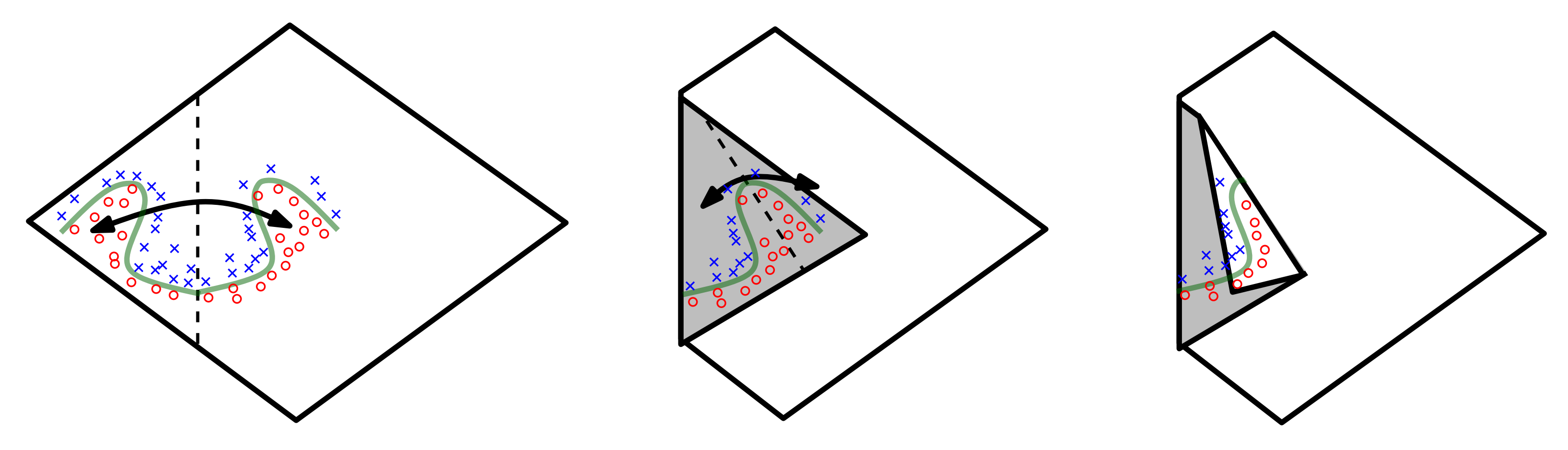
类似上图,每一次 ReLU 操作都相当于一次折纸操作,经过学习之后,网络仅仅通过这种折纸操作就可以学习”对称”这个概念。最终,使用一个比较简单的分类器就可以把 \(\color{blue}\times\) 和 \(\color{red}\circ\) 分开
在下图中,说明了神经网络中是怎么随着网络层数加深,最终,可以通过一个比较简单的函数实现分类。
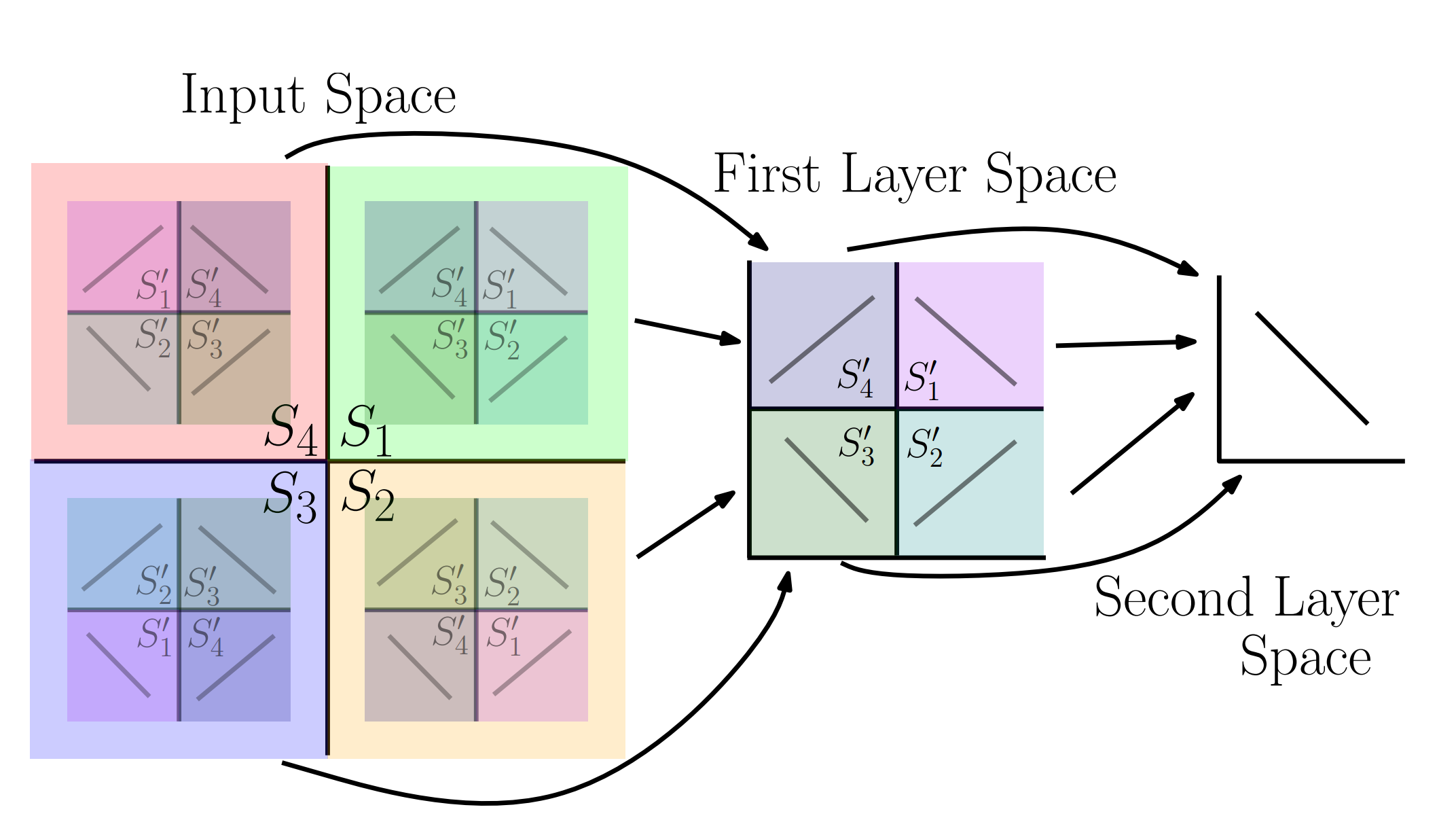
只要进行足够多次数的折叠,或者说,在神经网络中有足够多的层数,那么,使用 ReLU 函数,也可以近似任意的函数,而且,如果我们在最后一层使用一个 smooth 的函数,那么,整个神经网络就是一个真正的 smooth function approximator. 然而,在实际中,并不需要一个太 smooth 的 function approximator, 因为这容易导致 overfitting. 我们需要的是是在 test 数据集上表现好的模型,即要找的是 generalization 能力比较好的 approximator. 而 ReLU 这种仅仅 separate 样本空间的的函数,其本身自带 regularization 能力,所以,其泛化能力更强一些。因此,ReLU 是一个 reasonable 而且上佳的选择。
从这个角度讲,即使在全链接进行分类的最后几层,使用 ReLU 激活函数也是非常 reasonable 的。