深度学习中内存占用的优化
在深度学习中,我们总是希望能够训练更大,更深的网络模型。虽然硬件的发展速度很快,但是,为了构建更复杂的深层网络模型,总是希望有更多的显存 / 内存可用。对于同样的一个网络,如果能够使用更少的内存占用,也就意味着在训练的时候可以使用更大的 batch size, 通常也意味着更高的 GPU 使用率。
这篇文章讨论了深度学习中内存优化的问题,并且,给出了一些可能的解决方案。这些解决方案不一定是完备的,只是表示我们对这个问题的思考。
Computation Graph
首先要介绍一下 CG, 后续的讨论都会基于 CG. CG 描述了在神经网络中操作之间的 (数据流) 的依赖关系。图中的操作既可以是粗粒度的也可以是细粒度的。下图给出了两个例子。
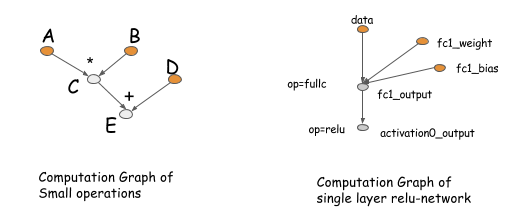
CG 的概念来源于 Theano, CGT 中,但是,在其他的一些深度学习库中,它们也以配置文件的方式存在。在这些库之间,它们的主要却别是计算梯度的方式。主要有两种方式,一种是在原图上计算梯度,另外一种是通过明确的反向传播的路径进行计算。
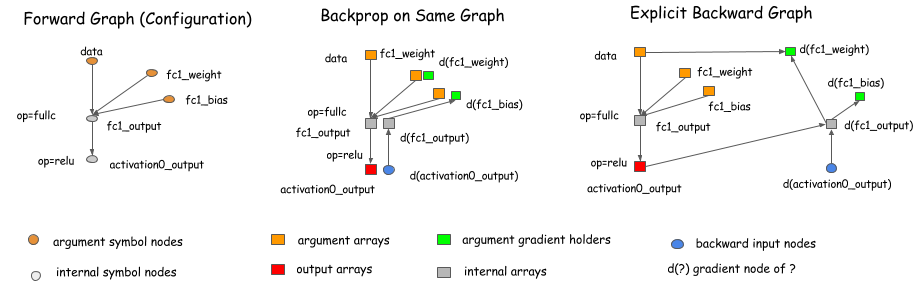
Caffe, Torch, CXXNet 是在原图上进行计算,Theano 和 CGT 有显式的反向传播路径。在这里,我们使用显示反向传播路径的图进行讨论.(因为,对于优化问题,它有诸多有点)
需要强调的一点是,使用显式的反向传播路径并没有把讨论局限于符号式的库 (symbolic library), 例如 Theano, CGT. 显式反向传播图同样适用于 layer-based library (layer-based library 会把 forward 和 backward 绑定到一起). 下图展示了这个过程是如何进行的。简单来说,我们引入了一个 backward 节点,而且这个节点连接到 forward 节点,在 backward 阶段调用 layer.backward
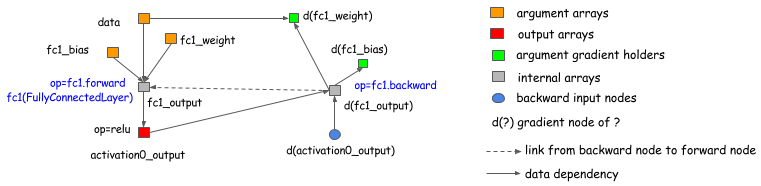
这篇讨论目前适用于几乎所有的深度学习框架 (当然会有类似于高阶微分这样的区别,但是,这些不在本文的讨论范围之内)
为什么说显式反向传播路径会更好呢?我们用两个例子来说明。首先,显式传播路径能够清晰的描述操作之间的依赖关系。例如下图,想计算 A 和 B 的梯度。从图中可以明确地看出,C 的梯度 d(C) 不依赖于 F, 这就意味着,对于 F 来说,一旦 forward 计算完成,可以马上释放 F 占用的内存空间。类似的 C 也可以被释放。
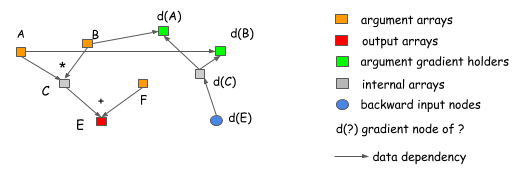
第二个优点是,显式反向传播路径可以有完全不同的反向传播路径,而不仅仅是 forward 的镜像。例如分割连接的例子,如下图:
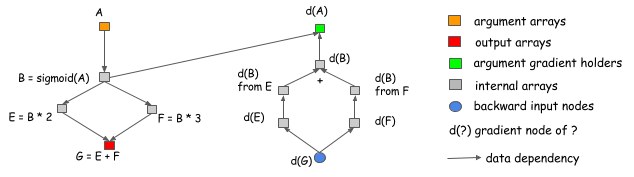
由图可知,输出 B 被两个操作使用,如果我们想在原图中计算梯度,那么就需要引入一个 split layer, 这也以为这在 forward 的时候也许需要这样的 split layer. 在这个例子中,forward 过程没有 split layer, 但是,这个图会在把梯度传给 B 之前自动插入一个 gradient aggregation node. 这就节省了 split layer 输出的内存和 forward 过程中复制数据的操作开销。
如果采用显式反向传播的方式,在 forward 和 backward 过程中就没有什么差别,只需要按照时间顺序处理计算图,而且也使得本文的讨论更清晰。现在的问题是,怎样为计算图中每一个输出节点分配显存呢?
这个问题似乎和深度学习没有关系,更多的是和编译,数据流优化有关。主要是深度学习这个重要的问题促使我们研究这个问题,并且从中受益。
What Can Be Optimized
希望读者现在能体会到计算图是讨论内存优化的一个比较好的工具。上文中已经可以看到,通过显式的反向传播路径可以实现一些内存优化,现在需要进一步探索这个问题。
假设我们需要构建一个 n 层的神经网络,通常来讲,需要为每一层的输出和梯度提供存储空间,错略来讲是 2n 的存储空间。在显式反向传播图中也是应该是大约 2n 的空间,因为在 backward 中的节点数和 forward 中的节点数大致相等。
In-Place Operations
内存优化中首先第一件可以做的事情是,对于 In-Place 的 operation 可以进行内存共享。通常对于简单的激活函数可以使用这个策略。例如下面这个例子,目的是计算三个链式的 sigmoid 激活函数。
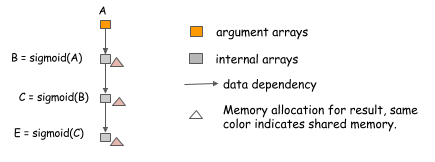
对于 sigmoid 函数可以进行 In-Place 计算,也就是说,输入和输入可以共享同一块内存,这时,只需要分配一块内存,就可以计算任意长度的链式激活函数。
然而,In-Place 的优化在某些情况下也会遇到问题。例如下面的例子,B 不仅被 C 使用,而且还会被 F 用到。
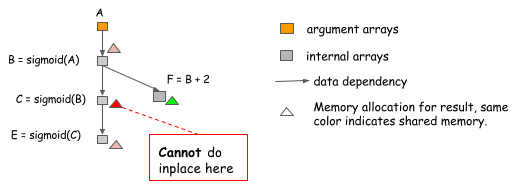
在计算过 C = sigmoid (B) 之后,B 仍然会被其他节点用到,因此,不能使用 In-Place 优化。因此,在代码中不能遇到 sigmoid 就使用 In-Place 优化,需要认真分析操作依赖。
Standard Memory Sharing
除了 In-Place operator, 还有其它的内存共享的方法。在下面的这个例子中,计算 E 的时候不需要 B 参与,因此,可以把 E 的计算结果放到 B 中。
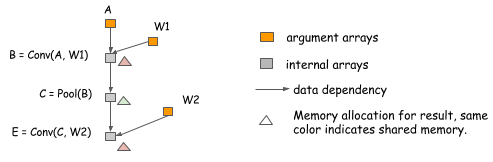
内存共享并不要求数据的内存占用是相同的,只需要在分配的时候,分配内存占用量的上确界,然后,所有操作共享这块内存。
Example of Real Neural Network Allocation
上面的例子都是为了说明概念,生造出来的一些例子。但是,方法同样可以应用到神经网络中。下图是一个两层的感知机的内存分配:
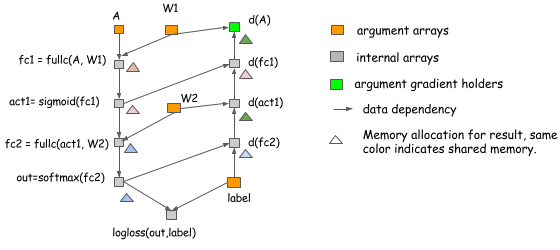
在上面这个例子中:
act1,d(fc1),out和d(fc2)是 In-Place 操作d(act1)和d(A)共享内存。
Memory Allocation Algorithm
到此为止,我们已经讨论过了内存优化的一些常见方法。其中有一些问题需要注意,例如在 In-Place 操作中提到的一个当前节点被多个其它节点依赖的情况。现在,方案是有了,具体要怎么实施呢?这并不是一个全新的问题,例如在编译器的寄存器的分配中就有类似的问题,因此,我们可以借鉴其中的一些思路。本文不会对该技术做非常详尽的分析,只是介绍一些非常有用的技巧来搞定内存优化的问题。
解决这个问题的核心是解决资源的冲突问题。具体来讲,就是任何一个变量都有一个生命周期 (life time), 即其第一次进行计算到其最后一次被使用到。在多层感知机的例子中,fc1 的生命周期在 act1 计算完成之后就结束了。

内存共享的原则是共享内存的变量的生命周期不会相互重叠。有多种方法可以实现这个目的。例如可以通过构建冲突图的方法,图中的每一个节点表示一个变量,生命周期有重叠的变量之间相互连接,然后在这个图上运行图染色算法,时间复杂度大约是 \(O (n^2)\), 其中,n 是图中节点的个数。这个计算复杂度还是比较大的。
下面介绍一个启发式的算法,其思想的模拟图遍历,并且给当前节点维护一个计数器 (counter), 计数器的数值是依赖于该节点并且尚未完成操作的的节点数量
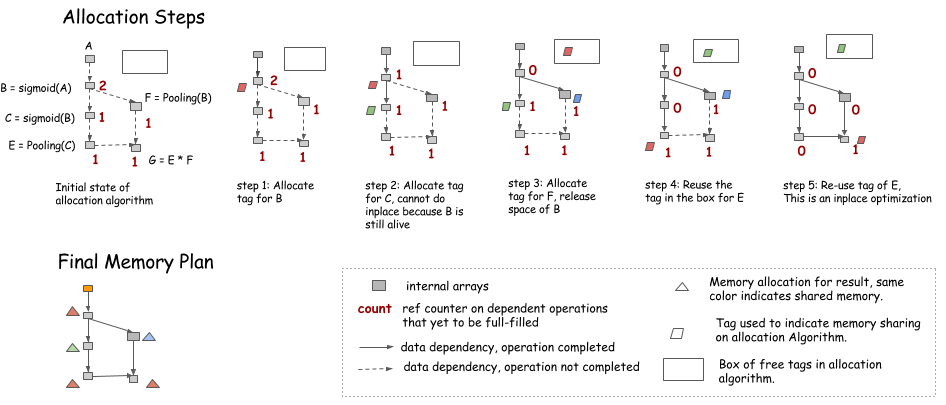
- 在出度为 1 的节点上可以进行 In-Place 操作
- 在 counter==0 之后可以把内存回收 (放到右上角的矩形框中)
- 需要新内存的时候,要么从右上角矩形框中取,要么申请新的内存。
注意:在上面的模拟中,并没有真正分配内存,而是记录下来每个节点需要多少内存,然后,在模拟完成之后,一次性进行内存申请,申请内存大小是内需需求的上确界.(这是因为,每次申请内存的开销是一样的,与其每个节点都申请 (或释放) 内存,不如,最后一次性把所需要的内存全部申请到)
Static vs. Dynamic Allocation
上面的策略准确模拟了交互式语言如 Python 中的内存分配过程。其中 counter 是其引用计数,当引用计数变成 0 的时候进行内存回收。从这个意义上说,我们使用动态内存分配的方法创建了一个静态内存分配方案。可是,是否可以完全动态的分配和回收内存了?
其中主要的不同是,静态的内存分配只需要做一次,因此,复杂的内存分配算法是可以接受的。例如,可以搜索与需求的内存大小相似的内存块。而且,内存的分配对图来说是可感知的 (下一节讲到). 如果使用动态内存分配,那么,就需要非常快速的内存分配和回收策略。
对于计划使用动态内存分配方法的情况,有个技巧是:永远不要做没有必要的对象引用。例如,把所有的节点组织成一个链表形式并且存储在图对象中,结果是,所有的节点的引用计数都不会被释放,并且没有存储空间。
Memory Allocation for Parallel Operations
前面讨论了如何对计算图进行静态的内存分配。但是,对于并行计算的内存优化会有新的问题,因为在并行计算中,资源的共享和并行计算是两个相互矛盾的状态。增加并行度意味着要减少资源共享,增加资源共享意味着要减少并行度。例如下面这个对于同一个图的两种不同的内存优化方案:
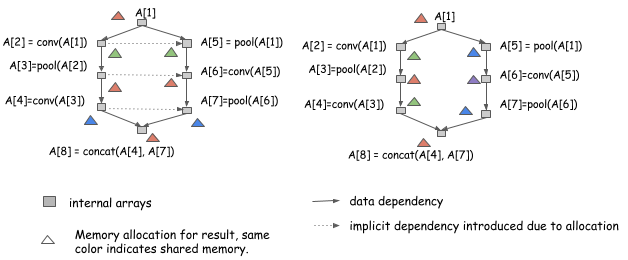
两个分配方案,如果顺序地计算 A [1] 到 A [8] 都是可行的,但是,如果考虑到并行的状态,右边的方案显然更好,因为,在左边的方案中,A [2] 和 A [5] 是无法并行的。
对于并行计算,需要夹被小心。
Be Correct and Safe First
内存分配的正确性。要求要考虑到隐式的内存共享中的依赖。一种解决方法是,把隐式的依赖加入到图中 (通过边的连接), 另外一种更直接的方案是,如果执行引擎是修改可感知的,直接把操作放到队列中,写入到相同的 variable tag 中 (相同的 tag 表示相同的内存区域)
内存分配的安全性。要求不要在可并行的节点之间进行内存共享。虽然在内存优化要求高的情况下这不是理想的选择,而且,在同一个 GPU 上有多个计算流的时候,优化带来的收益并不是很多。但是,这不失为保证安全性的一种简单有效的方法。
Try to Allow More Parallelization
通过以上讨论,现在可以比较安全的进行优化了。其中心思想是在无法并行的节点之间进行内存共享。其中一种方式是构建一个祖先关系图,然后在分配内存的时候搜索该图,这种方案的时间复杂度是 \(O (n^2)\). 另外一种方案是启发式的,例如对图中的边进行染色。如下图所示,在图中找到最长的路径,然后把这个路径涂相同的颜色,然后继续。
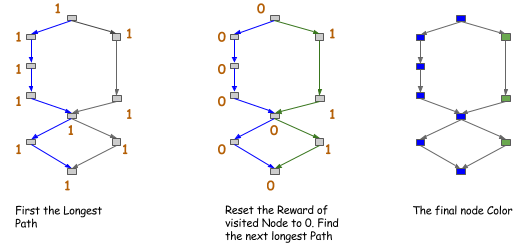
完成上色之后,只允许 (或者说鼓励) 颜色相同的节点之间进行共享。这是祖先图的更强条件的特例,但是,其找到前 k 个路径的时间复杂度只有 \(O (n)\)
这应该不是唯一的方法,其它的方式肯定也是存在的。
How Much Can you Save
上面讨论了深度学习模型内存压缩的方法,但是,具体的效果怎么样呢?
在应经对 big operator 进行优化的粗粒度的图中,上述方法大约可以节省一般的内存。如果使用优化了的 symbolic 的库的话,效果会更好。