NIN 是我读过的论文中几篇比较重要的之一,NIN 主要是贡献了 \(1 \times 1\) 的卷积这种玩法以及 global average pooling. 虽然 NIN 给出的模型没有 googlenet vgg16 / vgg19 等模型被大家大量的使用和 transfer learning, 但是,NIN 提出的这两个技术影响了后来的一大批卷积神经网络模型。
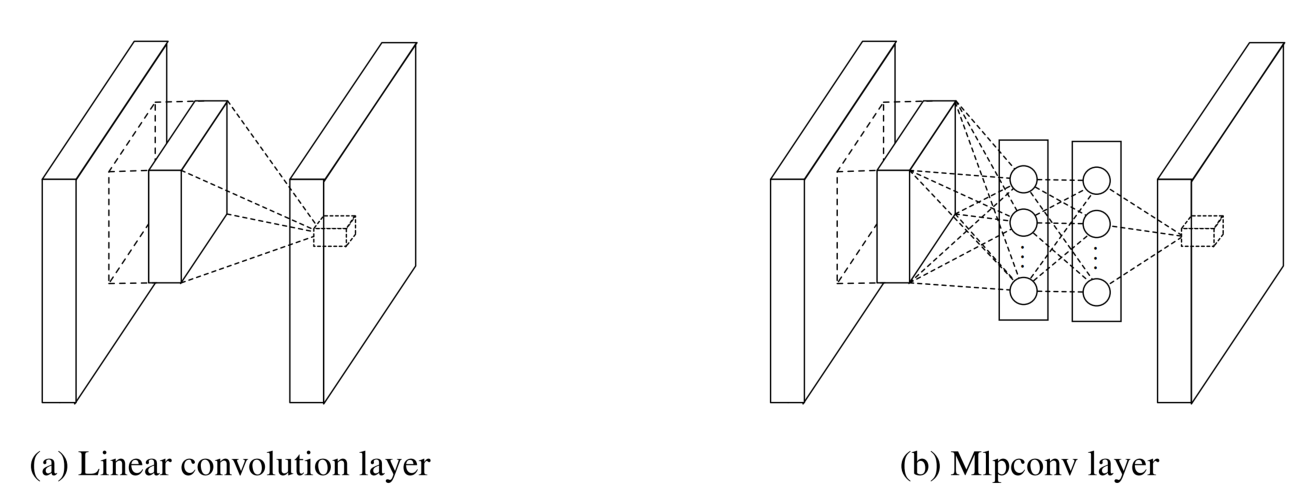
经典的卷积神经网络的结构一般是线性卷积 + Pooling + Full Connect, 在这篇文章中,作者认为,在图像识别中要提取的特征常常是非线性的,因此,使用线性的卷积显然无法满足要求。在传统的 CNN 中,为了使用线性卷积去提取非线性特征,常常需要使用大量的线性卷积,这样带来的后果是计算量的大幅增加。NIN 的工作中,为了解决这个问题,作者把线性的卷积改成非线性的卷积。其实,所谓的非线性卷积也是非常简单就能实现:在线性的卷积后面增加一个非线性的映射。
MLP Convolution Layers 如上图 a 是传统的卷积,其表示为 (以 ReLU 为例):
$$
f_{i,j,k}=max\left(w_k^Tx_{i,j},0\right)
$$
在 MLP Convolution 中为:
$$
\begin{align}
f_{i,j,k_1}^1 &=max\left({w_{k_1}^1}^Tx_{i,j}+b_{k_1}, 0\right) \\
\vdots \vdots\\
f_{i,j,k_n}^1 &=max\left({w_{k_n}^n}^Tf_{i,j}^{n-1}+b_{k_n}, 0\right)
\end{align}
$$
从上面的数学表达式看上去很复杂,也不好理解,这里给出 caffe 格式网络定义应该更容易理解:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 # 前面是正常的卷积操作 # 这里是mlp conv, 可以看出就是一个1 *1 的卷积操作(等价于全连接操作) layers { bottom: "conv1" top: "cccp1" name: "cccp1" type: CONVOLUTION blobs_lr: 1 blobs_lr: 2 weight_decay: 1 weight_decay: 0 convolution_param { num_output: 96 kernel_size: 1 stride: 1 weight_filler { type: "gaussian" mean: 0 std: 0.05 } bias_filler { type: "constant" value: 0 } } } # 接着接一个激活函数 layers { bottom: "cccp1" top: "cccp1" name: "relu1" type: RELU } # 在来一个用1 *1 的卷积完成的全连接操作 layers { bottom: "cccp1" top: "cccp2" name: "cccp2" type: CONVOLUTION blobs_lr: 1 blobs_lr: 2 weight_decay: 1 weight_decay: 0 convolution_param { num_output: 96 kernel_size: 1 stride: 1 weight_filler { type: "gaussian" mean: 0 std: 0.05 } bias_filler { type: "constant" value: 0 } } } # 接对应的激活函数 layers { bottom: "cccp2" top: "cccp2" name: "relu2" type: RELU } # 以上完成了两次非线性映射, 也就是 MLP 操作 layers { bottom: "cccp2" top: "pool0" name: "pool0" type: POOLING pooling_param { pool: MAX kernel_size: 3 stride: 2 } } layers { bottom: "pool0" top: "conv2" name: "conv2" type: CONVOLUTION blobs_lr: 1 blobs_lr: 2 weight_decay: 1 weight_decay: 0 convolution_param { num_output: 256 pad: 2 kernel_size: 5 stride: 1 weight_filler { type: "gaussian" mean: 0 std: 0.05 } bias_filler { type: "constant" value: 0 } } }
Global Average Pooling 对于常见的卷积神经网络,我一般把前面的卷积 + Pooling 操作看成是一个自动的特征提取器,然后后面的 Full Connect 看做是分类器,最后再接一个 softmax. 然而 Full Connect 由于参数太多,导致两个问题:
容易 overfitting (Drouput 是一种常见的 (标配) 解决这个问题的方法)
参数太多,计算资源需求非常高。
NIN 中提出了 global average pooling 来替代 fc, 所谓 gap 就是最后一层的整个 feature map 上面做 average pooling, 例如,最后一层 conv feature map 是 \(7 \times 7\), 那么,pooling 的 kernel 大小就是 \(7 \times 7\). 这样做的结果是完全不需要训练参数,而且还可以防止 overfitting. 在实践中,需要注意的是把最后一层的 conv kernel 个数设置为输出的类别数就可以了。例如在 ImageNet 中设置为 1000.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 layers { bottom: "cccp7" top: "cccp8" name: "cccp8-1024" type: CONVOLUTION blobs_lr: 1 blobs_lr: 2 weight_decay: 1 weight_decay: 0 convolution_param { # 注意设置最后一个feature map 的输出个数等于类别数 num_output: 1000 kernel_size: 1 stride: 1 weight_filler { type: "gaussian" mean: 0 std: 0.01 } bias_filler { type: "constant" value: 0 } } } layers { bottom: "cccp8" top: "cccp8" name: "relu12" type: RELU } # Global Average Pooling layers { bottom: "cccp8" top: "pool4" name: "pool4" type: POOLING pooling_param { # 使用average pooling pool: AVE # kernel size 等于 feature map 的大小 kernel_size: 6 stride: 1 } }