常见机器学习名词

发表于 分类于 ，

记录机器学习中常见的名词的定义。

  • \(L_0\) 范数：向量中非零元素的个数，用 \(L_0\) 范数正则化的目的是稀疏，因为，最小化正则项意味着最小化非零元素的个数
    \(L_0\) 优化问题很难求解 (NP hard 问题)
  • \(L_1\) 范数：向量中各元素的绝对值之和。也叫 Lasso regularization.
    \(L_1\) 是 \(L_0\) 的最优凸近似。
    任意一个 Lasso, 如果在 \(W_i = 0\) 的地方不可微，并且可以写成” 求和” 的形式，那么，这个 Lasso 就可以实现稀疏。

在一定条件下，\(L_1\) 在概率 1 的意义下等价于 \(L_0\)

  • \(L_2\) 范数：各元素求平方和然后开根号。回归里面叫做 Ridge Regression. 另外也称为 weight decay. 改善 overfitting
  • 欧氏距离 (Euclidean Distance)
\[ d_{12}=\sqrt{\left(a-b\right)\left(a-b\right)^T} \]
  • 曼哈顿距离 (Manhattan Distance)
    考虑在曼哈顿路口 A 到路口 B 的开车距离
\[ d_{12}=\sum_{k=1}^k \left\vert x_{1k}-x_{2k} \right\vert \]
  • 切比雪夫距离 (Chebyshev Distance)
\[ d_{12}=max_i{\left\vert x_{1i}-x_{2i} \right\vert} \]
  • Precision
\[ P = \frac{TP}{\left(TP+FP\right)} \]
  • Recall
\[ R = \frac{TP}{\left(TP+FN\right)} \]
  • F1 / F score
\[ F1 = \dfrac{2}{\dfrac{1}{P}+\dfrac{1}{R}} \]
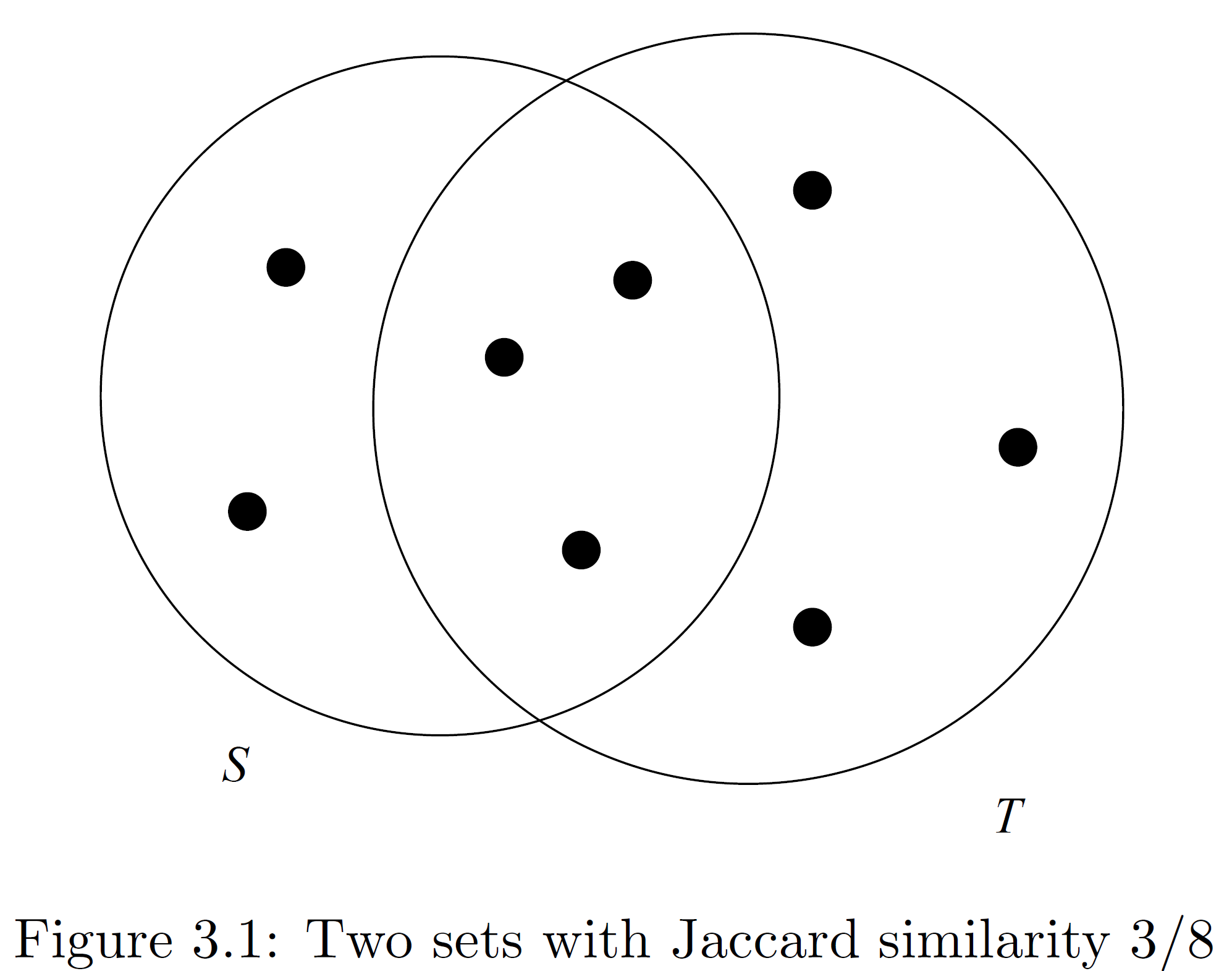
  • Jaccard similarity
    两个集合 \(S\) 和 \(T\) 的 Jaccard similarity 为：
\[ \mathrm{sim}(S, T) = \dfrac{S \cap T}{S \cup T} \]

举例如下图：