Memo
0%

Deep Knowledge Tracing

发表于 分类于 ，

学情跟踪是一个比较典型的时间序列的数据分析和预测。其目的是根据之前的学习情况，对学生的学习情况进行建模。虽然这里描述的是学情跟踪建模，但是，接下来描述的算法同样适用于其它的类似的场景，例如股票涨跌情况预测。
在这一类应用场景中，与其它应用最重要的一个区别是，该类应用需要预测每一个输出位置的概率。例如，需要预测每一只股票的涨跌。而其它场景需要预测的一般都是 one hot 类型。

这里使用的是 LSTM, 具体的 LSTM 是什么或者 RNN 是什么不是这篇的目的。
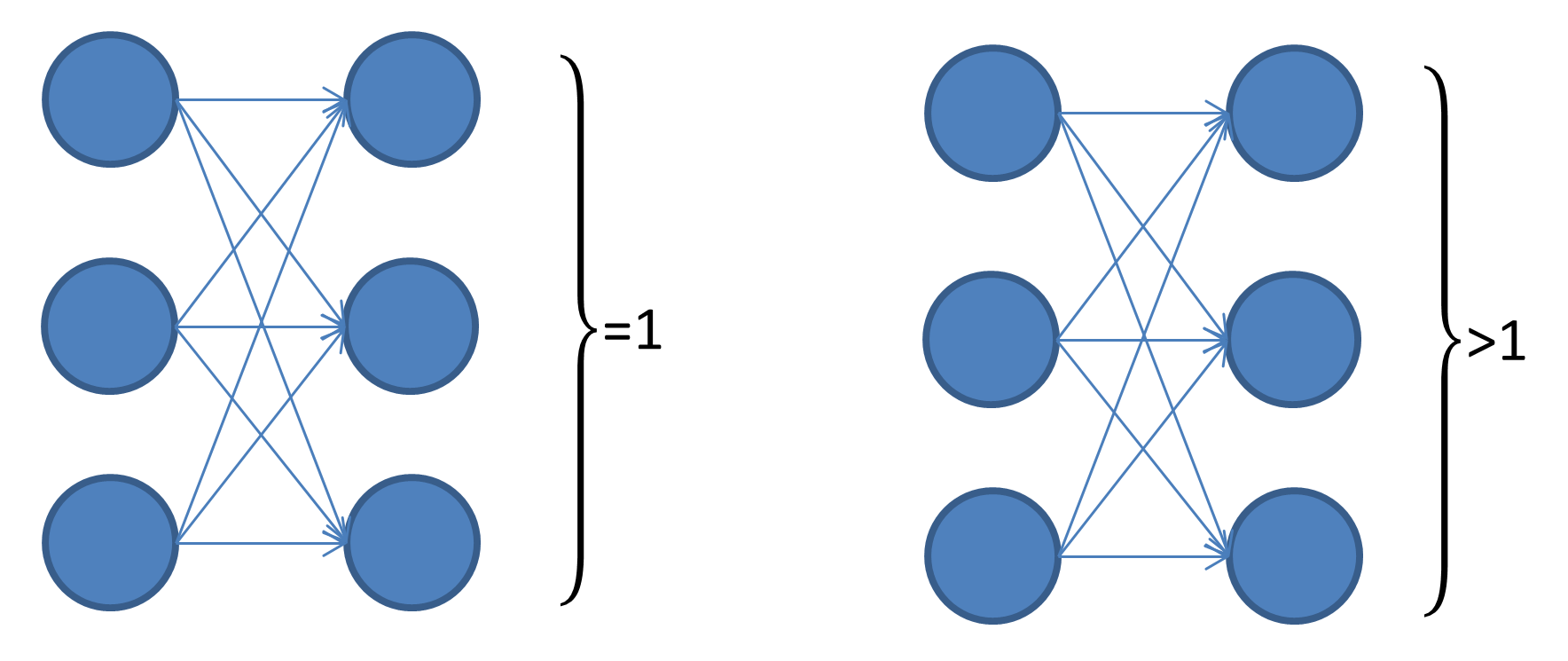
如下图左，输出节点使用 softmax 做映射，结果就是所有输出的和为 1. 如果输出节点记为 \(O_0,\cdots, O_{n-1}\), \(\sum_{i=0}^{n-1}p\left(O_i\right)=1\). 下图右即为这里要讨论的情形，在每一个输出节点上分别使用 sigmoid 做映射，即对于任意一个输出节点，\(p(O_i=0)+p(O_i=1)=1\).

既然输出变了，那么，相应的 loss function 也会随之改变，就不能用常见的 softmax 的 cross entropy loss 了。在这里，使用的 sigmoid 二分类的 loss function. 具体的方法是有一点点小 trick 的。
另外，要解释一下输入数据，我们拿到的数据学生历史做题对错情况，那么对于输入，一个比较简单的编码就是取一个向量，假设共有 N 各题目，那么，向量的长度为 2N, 如果，在一个 timestep 上，表现为正 (做对题，股票涨等), 该向量的 第 i 各位置为 1, 其余为 0, 否则，第 i+N 位置为 1, 其余为 0.
输出节点个数是 N, 每一个节点表示的是这道题目做对的概率。

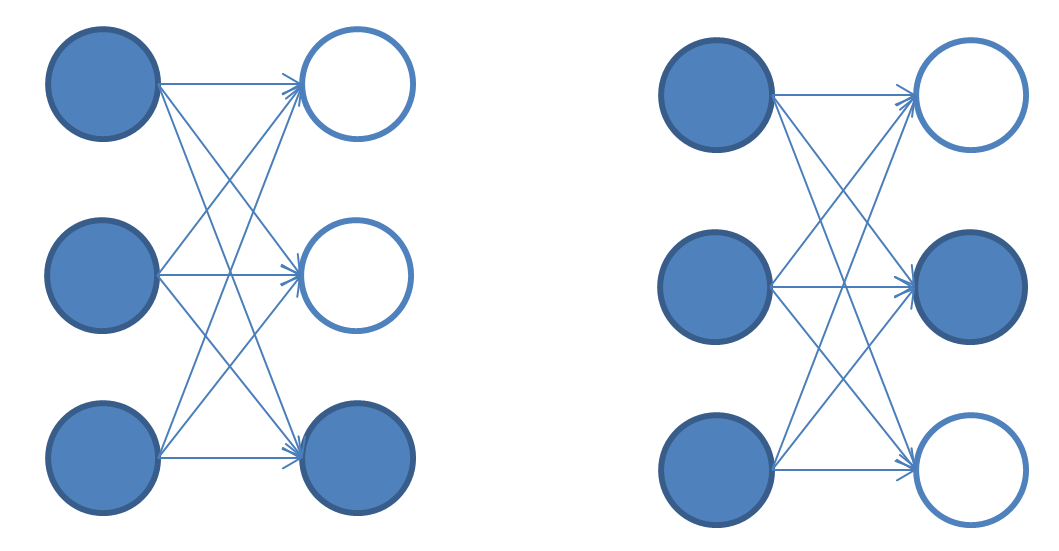
损失函数是这个工作中最最重要的地方，在每一次 forward 之后，会在相应的输出打上 mask, 例如，输入是第 i 只股票，那么，只看第 i 各输出节点，计算其 loss, 其它所有的节点都不看。如下图，第一次输入的是第 3 各学生的做题情况，那么，只激活第 3 各输出节点，第二次输入的是第 2 个学生的做题情况，那么，只激活第 2 个输出节点。

\[ L = \sum_t l\left(y^T \sigma\left(q_{t+1}\right), a_{t+1}\right) \]

其中，\(y^T\) 就是上面说到的 mask.
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import tensorflow as tf
x = tf.placeholder(tf.float32, [None, n_steps, n_input])
y = tf.placeholder(tf.float32, [None, n_steps])
skill = tf.placeholder(tf.float32, [None, n_steps, n_classes])
seqlens = tf.placeholder(tf.int32, [None, ])
keep_prob = tf.placeholder(tf.float32)
weights = tf.Variable(tf.random_normal([n_hidden, n_classes]))
weights = tf.get_variable("weights", shape=[n_hidden, n_classes], initializer=tf.contrib.layers.variance_scaling_initializer(factor=2.0, mode="FAN_IN"))
biases = tf.Variable(tf.zeros([n_classes]))
def dynamicRNN(x, n_steps):
    # data input shape (batch_size, n_steps, n_input)
    # convert to n_steps tensors list of shape(batch_size, n_input)
    x = tf.transpose(x, [1, 0, 2])
    # x = tf.sparse_tensor_to_dense(x)
    x = tf.reshape(x, [-1, n_input])
    x = tf.split(0, n_steps, x)
    lstm_cell = tf.nn.rnn_cell.GRUCell(n_hidden)
    lstm_cell = tf.nn.rnn_cell.DropoutWrapper(
        lstm_cell, output_keep_prob=keep_prob)
    outputs, states = tf.nn.rnn(
        lstm_cell, x, dtype=tf.float32, sequence_length=seqlens)
    outputs = tf.pack(outputs)
    # (batch_size, n_step, n_output)
    outputs = tf.transpose(outputs, [1, 0, 2])
    batch_size = tf.shape(outputs)[0]
    # (batch_size*n_step, n_output)
    outputs = tf.reshape(outputs, [-1, n_hidden])
    outputs = tf.matmul(outputs, weights)+biases
    outputs = tf.reshape(outputs, [batch_size, n_steps, n_classes])
    # 给输出打上 mask, 获取目标输出
    outputs = tf.reduce_sum(skill*outputs, axis=2)
    loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(outputs, y))
    # accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.round(tf.sigmoid(outputs)), y), tf.float32))
    predict = (tf.sigmoid(outputs))
    # learning_rate = tf.train.exponential_decay(learning_rate=0.1, global_step=tf.Variable(0, trainable=False), decay_steps=3578, decay_rate=0.96, staircase=True)
    optimizer = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss)
    return optimizer, loss, predict, outputs